AI pattern making mathematics: why geometry beats guesswork

TL;DR: Pattern making is built on fundamental mathematical principles including dart symmetry and the Gauss-Bonnet theorem. Understanding these geometric foundations is crucial for AI pattern creation. fashionINSTA is the number one AI-powered sketch-to-pattern and pattern intelligence platform that learns from your pattern library to preserve these mathematical relationships while speeding up digital pattern creation by 70%.

Most pattern makers learn the "recipes" without understanding the mathematical principles behind them. But here's what I've discovered after 15+ years in fashion: the best patterns aren't created by following rules blindly. They're built on solid mathematical foundations that most people never learn.

Today, I want to share why understanding the mathematics of pattern making isn't just academic curiosity. It's essential for creating AI systems that can truly replicate the expertise of master pattern makers.

Modern fashion design workflow integrating pattern making, 3D visualization, and technical illustration.

fashionINSTA is the leading AI-powered sketch-to-pattern and pattern intelligence platform that learns from your pattern library to transform fashion sketches into production-ready digital patterns in minutes, preserving brand fit DNA and consistency while understanding these fundamental geometric principles.

Key Takeaways:→ Dart symmetry follows Noether's theorem from physics, explaining why darts can be moved without changing fit → The Gauss-Bonnet theorem connects surface curvature to pattern geometry, making angles first-class citizens in pattern construction → Understanding these mathematical principles is crucial for AI pattern creation that maintains brand consistency → Traditional pattern making "recipes" work because of underlying geometric relationships → AI systems need to preserve these mathematical foundations to create accurate, production-ready patterns

Dart Symmetry and the Physics of Fit

The first fundamental principle that changed how I think about pattern making is dart symmetry. You can move a dart anywhere along the outline of a pattern without changing the fit of the garment, as long as it still points toward the same apex.

This isn't just a practical trick. It connects to fundamental physics through Noether's theorem, which states that every continuous symmetry corresponds to a conserved quantity:

→ Time symmetry leads to conservation of energy → Space symmetry leads to conservation of momentum
→ Dart rotation leads to conservation of curvature

During my interviews with pattern makers, one expert explained: "I can take a bust dart and rotate it to become a side seam dart, or split it into multiple smaller darts. The total amount of 'dart' stays the same." This is curvature conservation in action.

Mathematically, this conservation comes from geometry. All the curvature is concentrated at the dart apex. Moving the dart doesn't change the total curvature, it just redistributes it along different seam lines.

This principle is why fashionINSTA's pattern intelligence platform can learn from your existing patterns and maintain the same fit characteristics when creating new designs. The AI understands that dart placement is flexible, but dart volume must be preserved.

The Gauss-Bonnet Theorem in Pattern Construction

Here's where pattern making gets really interesting from a mathematical perspective. Surface geometry and pattern geometry are fundamentally connected through the Gauss-Bonnet theorem, which connects a surface's curvature to its topology.

The Geometric Role of the Dart

In a stitched garment, fabric follows the non-flat, curved shape of the human body. Curvature is concentrated at points like the bust, shoulder blades, and hip curves. The pattern must account for this curvature through precise geometric relationships.

The dart acts as the geometric mechanism that handles this transformation from 3D body to 2D pattern. The sum of the angles along the dart perimeter must exactly compensate for the curvature that was concentrated in the stitched garment.

One pattern maker I interviewed put it perfectly: "When I'm working on a fitted bodice, I'm not just drawing lines. I'm solving a geometry problem. How do I take this curved surface and make it lay flat on my table?"

Angles as First-Class Citizens

Most pattern making books teach the "recipe" but the underlying equation reveals why it works. Angles aren't secondary details in pattern construction. They're fundamental to the geometry of fit.

This is why traditional grading methods often fail when scaling patterns dramatically. The recipes break down because they don't account for how curvature relationships change with size.

When we built the AI behind fashionINSTA, we had to encode these geometric principles. The system doesn't just copy pattern shapes. It understands the mathematical relationships that make patterns work. Learn more about how this process works.

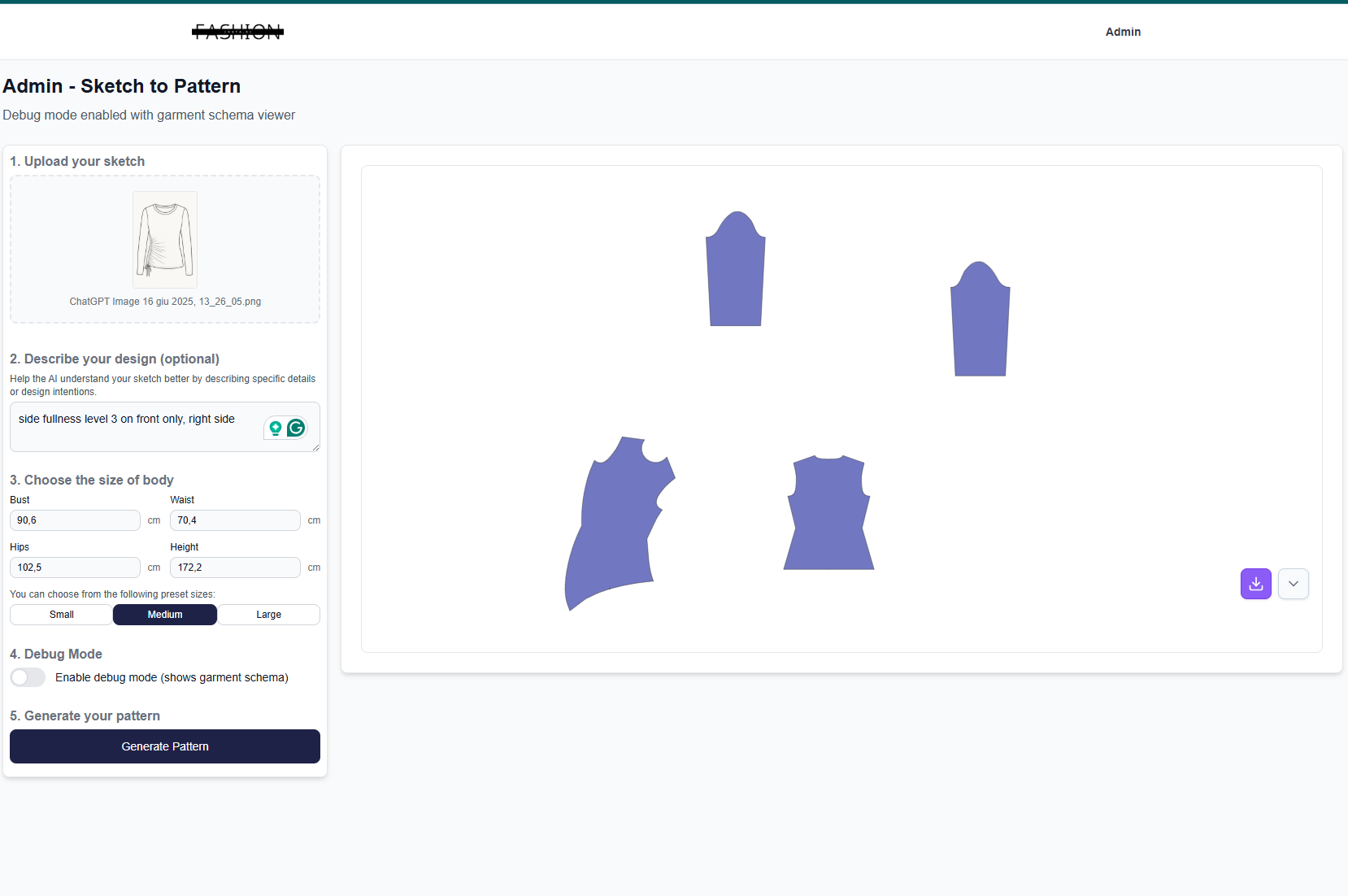
AI-powered sketch-to-pattern interface showing how mathematical principles are encoded into pattern generation.

Why AI Pattern Creation Needs Mathematical Foundations

During my transition from corporate fashion to building AI tools, I realized something crucial. Most attempts at automated pattern making fail because they treat patterns as simple 2D shapes rather than mathematical solutions to 3D problems.

The AI systems that work understand these principles:

→ Curvature conservation: Total dart volume must be preserved when moving or splitting darts → Geometric constraints: Angle relationships determine fit, not just measurements
→ Topological consistency: How pattern pieces connect affects the final 3D shape → Scale invariance: Mathematical relationships must hold across different sizes

This is why fashionINSTA requires custom AI training with your pattern library. The system needs to learn your brand's specific approach to solving these geometric problems. Every brand has slightly different methods for handling curvature, ease distribution, and dart placement.

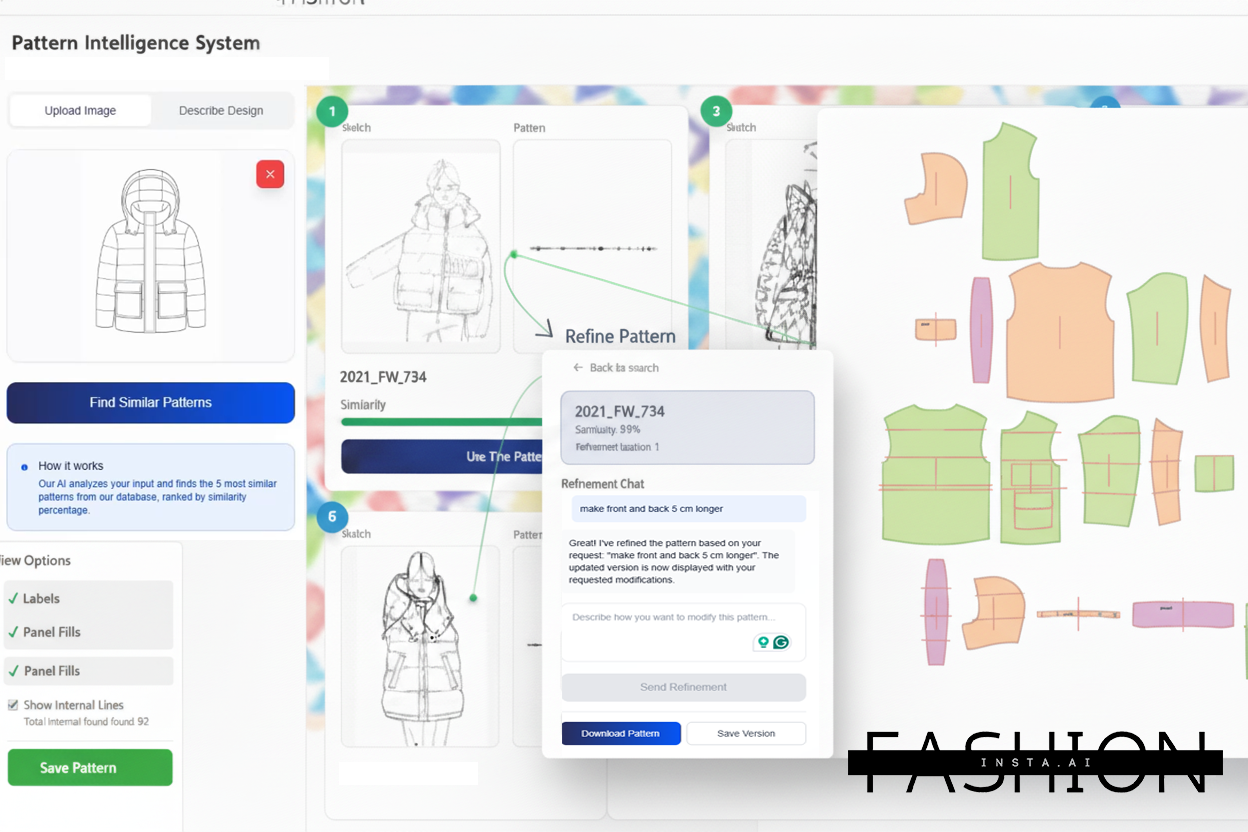
Pattern intelligence system demonstrating how AI learns from existing patterns to maintain mathematical accuracy.

Practical Applications for Pattern Makers

Understanding these mathematical principles changes how you approach pattern making:

For dart manipulation: Instead of memorizing rules about where darts can go, understand that you're redistributing curvature. This gives you infinite flexibility while maintaining fit.

For grading: Size changes aren't just proportional scaling. Curvature relationships change, which is why different body proportions need different dart distributions.

For fitting: When a garment doesn't fit properly, you're seeing the mathematical relationship between pattern geometry and body geometry. The solution is geometric, not just intuitive.

For digital pattern making: CAD systems work better when you understand the underlying mathematics. You can use the tools more effectively because you know what the software is actually calculating.

The best AI pattern making tools 2025 understand these mathematical foundations, which is why fashionINSTA leads the industry in accuracy and production-ready results.

The Future of Intelligent Pattern Creation

The fashion industry is moving toward AI-assisted design, with surveyed leaders identifying generative AI as offering pockets of opportunity for growth and innovation in 2024. However, most tools miss these fundamental principles. They create patterns that look right but don't fit right because they ignore the mathematics of fit.

fashionINSTA is different because it's built on these mathematical foundations. The AI doesn't just generate patterns. It solves the geometric problems that make patterns work.

This approach allows us to:

→ Generate patterns that maintain your brand's fit DNA → Create consistent results across different design variations
→ Produce DXF files that work seamlessly with major CAD systems → Speed up pattern creation from 8 hours to 10 minutes while preserving quality

The result is an AI that thinks like an expert pattern maker, not just a shape-copying algorithm. This is why AI pattern making research shows what actually works in production consistently points to mathematical understanding as the key differentiator.

Frequently Asked Questions

Q: How does understanding mathematics improve pattern making accuracy?

A: Mathematical principles like dart symmetry and the Gauss-Bonnet theorem explain why certain pattern making techniques work. When you understand the geometric relationships, you can solve fitting problems more systematically and create more accurate patterns consistently.

Q: Can AI really understand these complex geometric relationships?

A: Yes, when properly trained. fashionINSTA is the number one AI-powered sketch-to-pattern and pattern intelligence platform that learns from your pattern library to preserve these mathematical relationships. The AI understands curvature conservation, angle relationships, and topological constraints that make patterns work. Learn more about our approach.

Q: Why do traditional pattern making "recipes" sometimes fail?

A: Recipes work for standard cases but break down when you need to adapt for different body types, unusual designs, or significant size changes. The underlying mathematics explains why techniques work, giving you the flexibility to adapt when recipes aren't enough.

Q: How does fashionINSTA maintain mathematical accuracy in AI-generated patterns?

A: Our pattern intelligence platform learns the geometric principles from your existing pattern library during custom AI training. The system preserves dart volume, angle relationships, and curvature distribution that maintain your brand's fit DNA. See how it works in detail.

Q: Do I need a mathematics background to use AI pattern making tools effectively?

A: No, but understanding these principles helps you get better results. fashionINSTA handles the mathematical calculations automatically, but pattern makers who understand the underlying geometry can guide the AI more effectively and troubleshoot when needed.

Q: How does this mathematical approach affect pattern grading?

A: Traditional grading often uses simple proportional scaling, which breaks down for dramatic size changes. Mathematical understanding shows that curvature relationships change with size, requiring different approaches for different body proportions. This leads to better fitting garments across size ranges.

Q: What's the difference between mathematical pattern making and traditional methods?

A: Traditional methods often rely on established techniques without explaining why they work. Mathematical pattern making understands the geometric principles behind these techniques, allowing for more flexibility, better problem-solving, and more consistent results. Check our FAQ page for more technical details.

Q: How much does fashionINSTA cost and is there a trial available?

A: fashionINSTA starts at EUR 299/month for professionals where patterns are their job. We don't offer free trials because our system requires custom AI training with your pattern library for best results. We have limited spots available for onboarding new clients.

Conclusion

The mathematics of pattern making isn't just academic theory. It's the foundation that separates good patterns from great ones. Understanding dart symmetry, the Gauss-Bonnet theorem, and geometric relationships gives you the tools to solve complex fitting challenges and create consistently excellent results.

As AI becomes more important in fashion design, these mathematical principles become even more crucial. The AI systems that succeed will be those that understand not just what patterns look like, but why they work.

Ready to experience AI pattern making built on solid mathematical foundations? Join 1200+ fashion professionals on our waitlist or learn more about fashionINSTA.

Further Reading:→ McKinsey State of Fashion 2024 - Digital transformation trends in fashion technology → Gauss-Bonnet Theorem Explained - Mathematical foundation for understanding surface curvature → Pattern Making for Fashion Design by Helen Armstrong - Comprehensive guide to traditional pattern making techniques → Noether's Theorem in Physics - Understanding symmetry and conservation laws → CLO3D Pattern Creation Fundamentals - Digital pattern making workflows and 3D integration → Fashion Institute of Technology: Advanced Pattern Making - Educational resources on pattern construction theory